# Example usage
n_max_modes = 25
m_max_modes = 25
radius = 1.0
n_gridpoints_r = 100
n_gridpoints_theta = 100
wavenumbers = drumhead_wavenumbers(n_max_modes, m_max_modes, radius)
eigenvalues = drumhead_eigenvalues(wavenumbers)
r = np.linspace(0, radius, n_gridpoints_r)
theta = np.linspace(0, 2 * np.pi, n_gridpoints_theta)
K_fwd, K_inv, K_N = drumhead_eigenfunctions(wavenumbers, r, theta)
assert K_inv.shape == (
n_max_modes,
m_max_modes,
n_gridpoints_r,
n_gridpoints_theta,
)
assert K_fwd.shape == (
n_max_modes,
m_max_modes,
n_gridpoints_r,
n_gridpoints_theta,
)Funtional Transformation Method Utilities
This notebook contains a set of utility functions for the functional transformation method.
StringParameters
StringParameters (A:float=5.188e-07, I:float=1.41e-13, rho:float=1140, E:int=5400000000.0, d1:float=8e-05, d3:float=1.4e-05, Ts0:float=60.97, length:float=0.65)
Dataclass to store the parameters of the string.
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: Unknown section Properties
else: warn(msg)PlateParameters
PlateParameters (h:float=0.0005, l1:float=0.2, l2:float=0.3, rho:float=7800.0, E:int=2000000000000.0, nu:float=0.3, d1:float=0.042, d3:float=0.0023, Ts0:float=100)
Physical parameters for a rectangular plate simulation.
CircularDrumHeadParameters
CircularDrumHeadParameters (h:float=0.00019, r0:float=0.328, I:float=5.7e-13, rho:float=1380.0, E:int=3500000000.0, nu:float=0.35, d1:float=0.14, d3:float=0.32, Ts0:float=3990, f0:float=143.95)
Kettle drum head, from Digital sound synthesis of string instruments with the functional transformation method Table 5.2.
string_eigenfunctions
string_eigenfunctions (wavenumbers:numpy.ndarray, grid:numpy.ndarray)
*Compute the modes of the string. The modes of the string are given by:
\[ K = \sin(\pi x k) \]
where \(k\) is the wavenumber and \(x\) is the grid positions.*
| Type | Details | |
|---|---|---|
| wavenumbers | ndarray | The wavenumbers of the string. |
| grid | ndarray | The grid positions of the string where to compute the modes. |
| Returns | ndarray | The modes of the string at the given grid positions. |
string_eigenvalues
string_eigenvalues (n_modes:int, length:float)
*Compute the eigenvalues of a string with fixed ends.
The eigenvalues are given by:
\[\lambda_\mu = \left(\frac{\mu \pi}{L}\right)^2\]
where \(\mu\) is the mode number and \(L\) is the length of the string.*
| Type | Details | |
|---|---|---|
| n_modes | int | Number of modes to compute |
| length | float | Length of the string |
| Returns | jnp.ndarray | Array of eigenvalues with shape (n_modes,) |
plate_eigenfunctions
plate_eigenfunctions (wavenumbers_x:numpy.ndarray, wavenumbers_y:numpy.ndarray, x:numpy.ndarray, y:numpy.ndarray)
*Compute the modes of the plate. The modes of the plate are given by:
\[ K = \sin(\pi x k) \sin(\pi y k) \]
where \(k\) is the wavenumber and \(x\) and \(y\) are the grid positions.*
| Type | Details | |
|---|---|---|
| wavenumbers_x | ndarray | (n_max_modes_x,) |
| wavenumbers_y | ndarray | (n_max_modes_y,) |
| x | ndarray | (n_gridpoints_x,) |
| y | ndarray | (n_gridpoints_y,) |
| Returns | ndarray |
plate_eigenvalues
plate_eigenvalues (wavenumbers_x:numpy.ndarray, wavenumbers_y:numpy.ndarray)
*Compute the eigenvalues of the plate. The eigenvalues of the plate are given by:
\[\begin{equation} \lambda_{\mu, \nu} = \left(\frac{\mu \pi}{L_1}\right)^2 + \left(\frac{\nu \pi}{L_2}\right)^2 \end{equation}\]
where \(\mu\) and \(\nu\) are the mode numbers and \(L_1\) and \(L_2\) are the width and height of the plate.*
| Type | Details | |
|---|---|---|
| wavenumbers_x | ndarray | (n_max_modes_x,) |
| wavenumbers_y | ndarray | (n_max_modes_y,) |
| Returns | np.ndarray | The eigenvalues |
plate_wavenumbers
plate_wavenumbers (n_max_modes_x:int, n_max_modes_y:int, l1:float, l2:float)
*Compute the wavenumbers of a rectangular plate with clamped edges.
The wavenumbers are given by:
\[k_x = \frac{\mu \pi}{L_1}, \quad k_y = \frac{\nu \pi}{L_2}\]
where \(\mu\) and \(\nu\) are the mode numbers, and \(L_1\) and \(L_2\) are the plate dimensions.*
| Type | Details | |
|---|---|---|
| n_max_modes_x | int | Number of modes in x direction |
| n_max_modes_y | int | Number of modes in y direction |
| l1 | float | Width of the plate |
| l2 | float | Height of the plate |
| Returns | tuple | Wavenumbers in x and y directions with shapes (n_max_modes_x,) and (n_max_modes_y,) |
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Parameters:
---------- in
Compute the modes of the drumhead.
The modes of the drumhead are given by the Bessel function times the sine/cosine of the angle....
else: warn(msg)
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Returns:
------- in
Compute the modes of the drumhead.
The modes of the drumhead are given by the Bessel function times the sine/cosine of the angle....
else: warn(msg)drumhead_eigenfunctions
drumhead_eigenfunctions (wavenumbers:numpy.ndarray, r:numpy.ndarray, theta:numpy.ndarray)
*Compute the modes of the drumhead. The modes of the drumhead are given by the Bessel function times the sine/cosine of the angle.
Parameters:
wavenumbers: np.ndarray The wavenumbers for the drumhead. r: np.ndarray Radial grid points. theta: np.ndarray Angular grid points.
Returns:
modes: np.ndarray The eigenfunctions for the drumhead.*
| Type | Details | |
|---|---|---|
| wavenumbers | ndarray | (n_max_modes, m_max_modes) |
| r | ndarray | (n_gridpoints_r) |
| theta | ndarray | (n_gridpoints_theta) |
| Returns | ndarray |
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Parameters:
---------- in
Compute the eigenvalues of the drumhead.
The eigenvalues of the drumhead are given by the square of the wavenumbers....
else: warn(msg)
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Returns:
------- in
Compute the eigenvalues of the drumhead.
The eigenvalues of the drumhead are given by the square of the wavenumbers....
else: warn(msg)drumhead_eigenvalues
drumhead_eigenvalues (wavenumbers:numpy.ndarray)
*Compute the eigenvalues of the drumhead. The eigenvalues of the drumhead are given by the square of the wavenumbers.
Parameters:
wavenumbers: np.ndarray The wavenumbers for the drumhead. squared: bool If True, return the squared eigenvalues.
Returns:
eigenvalues: np.ndarray The eigenvalues of the drumhead.*
| Type | Details | |
|---|---|---|
| wavenumbers | ndarray | (n_max_modes, m_max_modes) |
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Parameters:
---------- in
Compute the wavenumbers of the drumhead.
...
else: warn(msg)
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: potentially wrong underline length...
Returns:
------- in
Compute the wavenumbers of the drumhead.
...
else: warn(msg)drumhead_wavenumbers
drumhead_wavenumbers (n_max_modes:int, m_max_modes:int, radius:float)
*Compute the wavenumbers of the drumhead.
Parameters:
n_max_modes: int The number of angular modes. m_max_modes: int The number of radial modes. radius: float The radius of the drumhead.
Returns:
wavenumbers: np.ndarray The wavenumbers for the drumhead.*
dblintegral
dblintegral (integrand, x, y, method='simpson')
Compute the double integral of a function K over the domain x and y.
\[ K_{n,m}(r, \varphi) = \cos (n \varphi) J_n\left(\mu_{n, m} \frac{r}{R}\right) \]
where \(J_n\) is the Bessel function of the first kind of order \(n\), and \(\mu_{n, m}\) is the \(m\)-th root of the \(n\)-th order Bessel function of the first kind.
wnx, wny = plate_wavenumbers(n_max_modes_x, n_max_modes_y, length_x, length_y)
assert np.allclose(plate_eigenfunctions(wnx, wny, grid_x, grid_y), K)
assert np.allclose(plate_eigenvalues(wnx, wny), Lambda)/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: Unknown section Parameters:
else: warn(msg)
/home/diaz/projects/jaxdiffmodal_clean/.venv/lib/python3.11/site-packages/fastcore/docscrape.py:230: UserWarning: Unknown section Returns:
else: warn(msg)inverse_STL
inverse_STL (K:numpy.ndarray, u_bar:numpy.ndarray, length:float)
Compute the inverse STL transform using the formula of Rabenstein et al. (2000).
| Type | Details | |
|---|---|---|
| K | ndarray | (n_modes, n_gridpoints) |
| u_bar | ndarray | (n_modes, n_samples) or (n_modes,) |
| length | float | length of the string |
| Returns | ndarray |
forward_STL
forward_STL (K:numpy.ndarray, u:numpy.ndarray, dx:float)
Compute the forward STL transform. The integration is done using the trapezoidal rule.
| Type | Details | |
|---|---|---|
| K | ndarray | (n_modes, n_gridpoints) |
| u | ndarray | (n_gridpoints, n_samples) or (n_gridpoints,) |
| dx | float | grid spacing |
| Returns | ndarray | The transformed signal. Shape (n_modes, n_samples) or (n_modes,) |
inverse_STL_2d
inverse_STL_2d (K:numpy.ndarray, u_bar:numpy.ndarray, l1:float, l2:float)
Compute the inverse STL transform.
| Type | Details | |
|---|---|---|
| K | ndarray | (n_modes_x, n_modes_y, n_gridpoints_x, n_gridpoints_y) |
| u_bar | ndarray | (n_modes_x, n_modes_y, n_samples) or (n_modes_x, n_modes_y) |
| l1 | float | length in x |
| l2 | float | length in y |
| Returns | ndarray | The reconstructed signal. Shape (n_gridpoints, n_samples) or (n_gridpoints,) |
forward_STL_2d
forward_STL_2d (K:numpy.ndarray, u:numpy.ndarray, x:float, y:float, use_simpson:bool=False)
Compute the forward STL transform. The integration is done using the trapezoidal rule.
| Type | Default | Details | |
|---|---|---|---|
| K | ndarray | (n_modes_x, n_modes_y, n_gridpoints_x, n_gridpoints_y) | |
| u | ndarray | (n_gridpoints_x, n_gridpoints_y, n_samples) or (n_gridpoints_x, n_gridpoints_y) | |
| x | float | grid spacing | |
| y | float | grid spacing | |
| use_simpson | bool | False | |
| Returns | ndarray | The transformed signal. Shape (n_modes, n_samples) or (n_modes,) |
evaluate_rectangular_eigenfunctions
evaluate_rectangular_eigenfunctions (mn_indices:numpy.ndarray, position:numpy.ndarray, params:__main__.PlateParameters)
| Type | Details | |
|---|---|---|
| mn_indices | ndarray | (n_modes, 2) selected mode indices |
| position | ndarray | (2,) position to evaluate the eigenfunctions |
| params | PlateParameters | |
| Returns | ndarray | (n_modes,) mode gains of selected modes at the given position |
evaluate_string_eigenfunctions
evaluate_string_eigenfunctions (indices:numpy.ndarray, position:numpy.ndarray, params:__main__.StringParameters)
| Type | Details | |
|---|---|---|
| indices | ndarray | (n_modes,) selected mode indices |
| position | ndarray | (1,) position to evaluate the eigenfunctions |
| params | StringParameters | |
| Returns | ndarray | (n_modes,) mode gains of selected modes at the given position |
length_x = 1.08
length_y = 0.8
n_max_modes_x = 25
n_max_modes_y = 25
n_gridpoints_x = 100
n_gridpoints_y = 100
x = np.linspace(0, length_x, n_gridpoints_x)
y = np.linspace(0, length_y, n_gridpoints_y)
wnx, wny = plate_wavenumbers(
n_max_modes_x,
n_max_modes_y,
length_x,
length_y,
)
K = plate_eigenfunctions(wnx, wny, x, y)
g = 0.5 * K[2, 2] + 0.5 * K[3, 3]
bar_g = forward_STL_2d(K, g, x, y, use_simpson=True)
g_reconstructed = inverse_STL_2d(K, bar_g, length_x, length_y)
assert np.allclose(g, g_reconstructed, atol=1e-2)
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].imshow(g, origin="lower", aspect="auto")
ax[0].set_title("Original excitation")
ax[1].imshow(g_reconstructed, origin="lower", aspect="auto")
ax[1].set_title("Reconstructed excitation")Text(0.5, 1.0, 'Reconstructed excitation')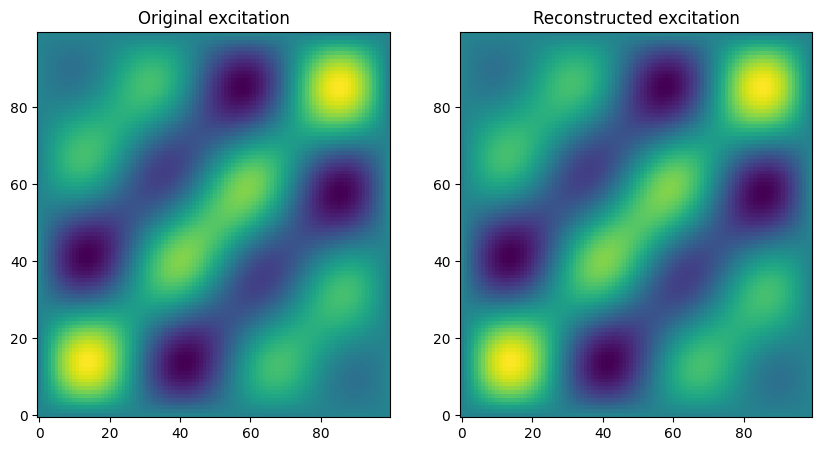
inverse_STL_drumhead
inverse_STL_drumhead (K_inv:numpy.ndarray, u_bar:numpy.ndarray)
Compute the inverse STL transform using the formula of Rabenstein et al. (2000).
| Type | Details | |
|---|---|---|
| K_inv | ndarray | (n_modes_x, n_modes_y, n_gridpoints_x, n_gridpoints_y) |
| u_bar | ndarray | (n_modes_x, n_modes_y, n_samples) or (n_modes_x, n_modes_y) |
| Returns | ndarray |
forward_STL_drumhead
forward_STL_drumhead (K:numpy.ndarray, u:numpy.ndarray, r:numpy.ndarray, theta:numpy.ndarray, use_simpson:bool=False)
Compute the forward STL transform. The integration is done using the trapezoidal rule or Simpson’s rule.
| Type | Default | Details | |
|---|---|---|---|
| K | ndarray | (n_modes_r, n_modes_theta, n_gridpoints_r, n_gridpoints_theta) | |
| u | ndarray | (n_gridpoints_x, n_gridpoints_y, n_samples) or (n_gridpoints_x, n_gridpoints_y) | |
| r | ndarray | radial grid | |
| theta | ndarray | angular grid | |
| use_simpson | bool | False | |
| Returns | ndarray |
# Example usage
n_max_modes = 10
m_max_modes = 10
radius = 1.0
n_gridpoints_r = 100
n_gridpoints_theta = 100
wavenumbers = drumhead_wavenumbers(n_max_modes, m_max_modes, radius)
eigenvalues = drumhead_eigenvalues(wavenumbers)
r = np.linspace(0, radius, n_gridpoints_r)
theta = np.linspace(0, 2 * np.pi, n_gridpoints_theta)
K_fwd, K_inv, K_N = drumhead_eigenfunctions(wavenumbers, r, theta)
assert np.allclose(
K_fwd.shape, (n_max_modes, m_max_modes, n_gridpoints_r, n_gridpoints_theta)
) # Should be (10, 10, 100, 100)
assert np.allclose(
K_inv.shape, (n_max_modes, m_max_modes, n_gridpoints_r, n_gridpoints_theta)
) # Should be (10, 10, 100, 100)
# Create an example g array to test the transforms
g = K_fwd[3, 3]
bar_g = forward_STL_drumhead(K_fwd, g, r, theta, use_simpson=False)
g_reconstructed = inverse_STL_drumhead(K_inv, bar_g)
# Verify if g can be reconstructed
assert np.allclose(g, g_reconstructed, atol=1e-2)
print(g.min(), g.max())
print(g_reconstructed.min(), g_reconstructed.max())
# Plot using pcolormesh
fig, ax = plt.subplots(
1,
2,
subplot_kw={"projection": "polar"},
figsize=(10, 5),
)
c = ax[0].pcolormesh(theta, r, g, shading="auto", cmap="viridis")
c = ax[1].pcolormesh(theta, r, g_reconstructed, shading="auto", cmap="viridis")-0.4320502477222054 0.43401550352665574
-0.4320519880367027 0.4340172517572766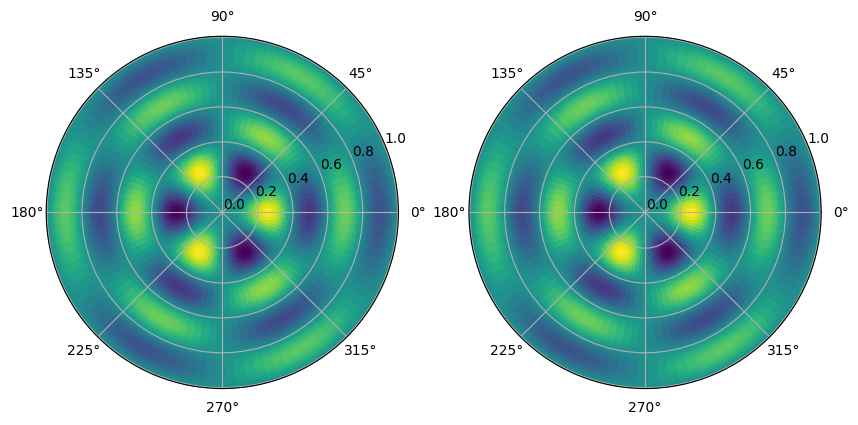
stiffness_term
stiffness_term (params:__main__.PhysicalParameters, lambda_mu:jax.Array)
damping_term_simple
damping_term_simple (lambda_mu:jax.Array, factor:float=0.001)
damping_term
damping_term (params:__main__.PhysicalParameters, lambda_mu:jax.Array)
eigenvalues_from_pde
eigenvalues_from_pde (pars:__main__.PhysicalParameters, lambda_mu:jax.Array)
Compute the positive imaginary side of the eigenvalues of the continuous-time system from the PDE parameters.
| Type | Details | |
|---|---|---|
| pars | PhysicalParameters | The physical parameters of the system. |
| lambda_mu | Array | The eigenvalues of the decompostion of the Laplacian operator. |
| Returns | Array | The eigenvalues of the continuous-time system. |
Some example use. Note that this is just a preview of how all the modes sound when excited at once. In a real setting they must be weighted with the eigenfunctions and the initial conditions or modal excitation.
n_max_modes = 30
sr = 44100
dt = 1 / sr
final_time = 1.0
n_samples = int(final_time / dt)
p_params = StringParameters()
lambda_mu = string_eigenvalues(n_max_modes, p_params.length)
eigvals = eigenvalues_from_pde(p_params, lambda_mu)
eigvals_d = np.exp(eigvals * dt)
states = np.vander(eigvals_d, n_samples, increasing=True).real
display(Audio(states.sum(0), rate=sr))sr = 44100
dt = 1 / sr
n_modes_x = 8
n_modes_y = 8
n_modes = n_modes_x * n_modes_y
final_time = 6.0
n_samples = int(final_time / dt)
p_params = PlateParameters()
wnx, wny = plate_wavenumbers(
n_max_modes_x,
n_max_modes_y,
p_params.l1,
p_params.l2,
)
lambda_mu = plate_eigenvalues(wnx, wny)
lambda_mu = np.sort(lambda_mu.reshape(-1))[:n_modes]
eigvals = eigenvalues_from_pde(p_params, lambda_mu)
eigvals_d = np.exp(eigvals * dt)
states = np.vander(eigvals_d, n_samples, increasing=True).real
display(Audio(states.sum(0), rate=sr))sr = 44100
dt = 1 / sr
n_modes_x = 8
n_modes_y = 8
n_modes = n_modes_x * n_modes_y
final_time = 2.0
n_samples = int(final_time / dt)
p_params = CircularDrumHeadParameters.avanzini()
wn = drumhead_wavenumbers(n_max_modes_x, n_max_modes_y, p_params.r0)
lambda_mu = np.sort(drumhead_eigenvalues(wn).reshape(-1))[:n_modes]
eigvals = eigenvalues_from_pde(p_params, lambda_mu)
eigvals_d = np.exp(eigvals * dt)
states = np.vander(eigvals_d, n_samples, increasing=True).real
display(Audio(states[0], rate=sr))sample_parallel_tf
sample_parallel_tf (num:numpy.ndarray, den:numpy.ndarray, dt:float, method:str='impulse')
Sample multiple transfer functions.
| Type | Default | Details | |
|---|---|---|---|
| num | ndarray | (n_modes,) | |
| den | ndarray | (n_modes,) | |
| dt | float | ||
| method | str | impulse | |
| Returns | np.ndarray | The numerator of the discrete-time transfer function. |
tf_initial_conditions_continuous_2
tf_initial_conditions_continuous_2 (D:float, density:float, d1:float, d3:float, Ts0:float, lambda_mu:<function array>)
Conpute the continuous-time initial condition transfer function. This is an alternative to the function tf_initial_conditions_continuous that eigenvalues of the PDE as input.
| Type | Details | |
|---|---|---|
| D | float | The bending stiffness of the string or plate. |
| density | float | The area or surface density of the string or plate. |
| d1 | float | The linear damping coefficient, or frequency-independent damping. |
| d3 | float | The cubic damping coefficient, or frequency-dependent damping. |
| Ts0 | float | The initial tension of the string or plate. |
| lambda_mu | array | The eigenvalues from the decomposition of the Laplacian operator. |
| Returns | tuple | The numerator and denominator of the transfer function. |
tf_excitation_discrete
tf_excitation_discrete (eigenvalues:numpy.ndarray, density:float, dt:float)
Compute the discrete-time excitation transfer function of a system.
| Type | Details | |
|---|---|---|
| eigenvalues | ndarray | The eigenvalues of the system. |
| density | float | surface or area density |
| dt | float | time step |
| Returns | tuple | The numerator of the discrete-time transfer function. |
tf_excitation_continuous
tf_excitation_continuous (eigenvalues:numpy.ndarray, density:float)
Compute the continuous excitation transfer function.
| Type | Details | |
|---|---|---|
| eigenvalues | ndarray | The eigenvalues of the system. |
| density | float | surface or area density |
| Returns | tuple | The numerator of the discrete-time transfer function. |
tf_initial_conditions_discrete
tf_initial_conditions_discrete (eigenvalues:numpy.ndarray, dt:float)
Compute the discrete-time initial conditions transfer function of a system.
| Type | Details | |
|---|---|---|
| eigenvalues | ndarray | The eigenvalues of the system. |
| dt | float | time step |
| Returns | tuple | The numerator of the discrete-time transfer function. |
tf_initial_conditions_continuous
tf_initial_conditions_continuous (eigenvalues:numpy.ndarray)
Compute the continuos “initial-conditions” transfer function from the eigenvalues of the system.
| Type | Details | |
|---|---|---|
| eigenvalues | ndarray | The eigenvalues of the system. |
| Returns | tuple | The numerator of the discrete-time transfer function. |
b, a = tf_excitation_discrete(eigvals, p_params.density, dt)
b_ic, a_ic = tf_initial_conditions_discrete(eigvals, dt)
# manual discretization
eigenvalues_d = np.exp(eigvals * dt)
# for the excitation tf
b1 = (
np.exp(eigvals.real * dt)
* np.sin(eigvals.imag * dt)
/ eigvals.imag
/ p_params.density
)
# for the initial conditions tf
# here we ignore initial velocity
r = np.exp(eigvals.real * dt)
b1_ic = r * np.sin(eigvals.imag * dt) / eigvals.imag * -eigvals.real - r * np.cos(
eigvals.imag * dt
)
a1 = -2 * np.exp(eigvals.real * dt) * np.cos(eigvals.imag * dt)
a2 = np.exp(2 * eigvals.real * dt)
b_manual = np.stack([np.zeros_like(b1), b1, np.zeros_like(b1)], axis=-1) * dt
a_manual = np.stack([np.ones_like(a1), a1, a2], axis=-1)
b_ic_manual = np.stack([np.ones_like(b1_ic), b1_ic], axis=-1) * dt
print(b[0])
print(b_manual[0])
print(b_ic[0] * sr)
print(b_ic_manual[0] * sr)
assert np.allclose(b[:, 1], b_manual[:, 1])
assert np.allclose(a, a_manual)
assert np.allclose(b_ic[:, :2], b_ic_manual[:, :2])[0.00000000e+00 1.90416682e-09 1.11022302e-16]
[0.00000000e+00 1.90416703e-09 0.00000000e+00]
[ 1.00000000e+00 -9.99682425e-01 2.93765012e-11]
[ 1. -0.99968243]