This notebook shows how to fit the physical parameters of a guitar string to a real recording.
Load a recording of a plucked guitar string.
Code
stiff_string_real, file_sr = sf.read("audio/G53-50205-1111-00019.wav")
if file_sr != sample_rate:
print(f"Resampling from {file_sr} to {sample_rate}")
stiff_string_real = soxr.resample(
stiff_string_real,
in_rate=file_sr,
out_rate=sample_rate,
)
print("The sample rate is", sample_rate)
duration = 1.0
offset = int(0.00 * file_sr)
stop = int(1 * file_sr)
stiff_string_real = stiff_string_real[offset : offset + stop]
u_stiff_string_rfft = np.fft.rfft(stiff_string_real)
Fit the real data using LPC to get an spectral envelope.
Code
a_lpc_cpu_solve_autocorr, g_lpc_solve_autocorr = lpc_cpu_solve(
stiff_string_real,
512,
method="autocorrelation",
biased=False,
)
w, h = freqz(
b=g_lpc_solve_autocorr,
a=np.concatenate([[1], a_lpc_cpu_solve_autocorr]),
worN=u_stiff_string_rfft.shape[0],
fs=sample_rate,
)
# impulse response
H = g_lpc_solve_autocorr / np.fft.rfft(
np.concatenate([[1], a_lpc_cpu_solve_autocorr]),
n=sample_rate,
)
y = np.fft.irfft(H, n=sample_rate)
y_rfft = np.abs(np.fft.rfft(y))
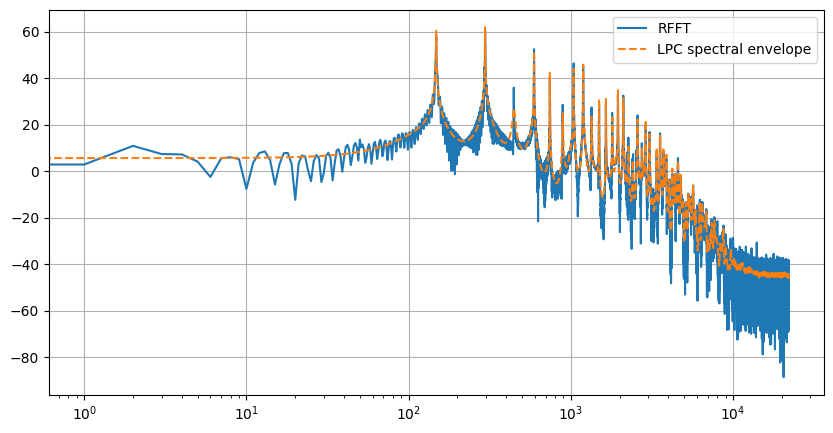
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.semilogx(w, to_db(np.abs(u_stiff_string_rfft)), label="RFFT")
ax.semilogx(w, to_db(np.abs(h)), label="LPC spectral envelope", ls="--")
ax.grid("both")
ax.legend()
display_audio_with_title(stiff_string_real, sample_rate, "Original")
display_audio_with_title(y, sample_rate, "LPC fit")
Original
LPC fit
Sample the envelope using the bark scale.
Code
hz_range = np.array([50, 15000])
melrange = hz2bark(hz_range)
worN = bark2hz(np.linspace(melrange[0], melrange[1], 20_000))
w, h = freqz(
g_lpc_solve_autocorr,
a=np.concatenate([[1], a_lpc_cpu_solve_autocorr]),
worN=worN,
fs=sample_rate,
)
h = jnp.abs(h) / jnp.max(jnp.abs(h))
Define the initial parameters and constraints.
Code
n_modes = 64
rng = np.random.default_rng(654)
pars = {
"bending_stiffness": rng.normal(scale=1e-3),
"gamma_mu": rng.uniform(size=(n_modes)),
"zero_radii": rng.normal(size=(n_modes)).astype(np.float32),
"zero_angles": rng.normal(size=(n_modes)).astype(np.float32),
"Ts0": rng.normal(scale=1e-3),
"length": 0.65,
"z0": rng.normal(size=(n_modes, 1)).astype(np.float32),
"gain": rng.normal(scale=1e-4),
}
def get_z0(params):
return jax.nn.sigmoid(params["z0"])
def get_gamma_mu(params):
return -jax.nn.relu(params["gamma_mu"])
# return -jnp.exp(params["gamma_mu"])
def get_radii(params):
return jax.nn.sigmoid(params["radii"])
def get_Ts0(params):
return jax.nn.sigmoid(params["Ts0"]) * 50_000
def get_gain(params):
return jax.nn.sigmoid(params["gain"]) * 0.001
def get_length(params):
return jax.nn.sigmoid(params["length"])
def get_bending_stiffness(params):
return jax.nn.sigmoid(params["bending_stiffness"]) * 10
def get_zero_radii(params):
return jax.nn.sigmoid(params["zero_radii"])
def get_zero_angles(params):
return jax.nn.sigmoid(params["zero_angles"])
def get_zeros(pars):
return jax.nn.sigmoid(pars["zero_radii"]) * jnp.exp(
2j * np.pi * jax.nn.sigmoid(pars["zero_angles"])
)
Simulate the string using the initial parameters.
Code
def tf_modified(
pars,
lambda_mu,
dt,
):
omega_mu_squared = (
get_bending_stiffness(pars) * lambda_mu**2 + get_Ts0(pars) * lambda_mu
)
gamma_mu = get_gamma_mu(pars)
omega_mu = jnp.sqrt(omega_mu_squared - gamma_mu**2)
# discretise
radius = jnp.exp(gamma_mu * dt)
real = radius * jnp.cos(omega_mu * dt)
zeros = get_zeros(pars)
b1 = -2.0 * zeros.real
b2 = zeros.real**2 + zeros.imag**2
a1 = -2.0 * real
a2 = radius**2
ones = jnp.ones_like(lambda_mu)
b = jnp.stack([ones, b1, b2], axis=-1)
a = jnp.stack([ones, a1, a2], axis=-1)
return b, a
def simulate_string(pars):
lambdas = string_eigenvalues(n_modes, length=get_length(pars))
b, a = tf_modified(pars, lambdas, dt)
b = b * get_z0(pars) * get_gain(pars)
h = tf_freqz(b, a, worN, sample_rate)
pred_freq_response = jnp.mean(jnp.abs(h), axis=0)
return pred_freq_response, b, a
initial_freq_response, b, a = simulate_string(pars)
u_stiff_string_rfft = np.fft.rfft(stiff_string_real)
fft_freqs = np.fft.rfftfreq(len(stiff_string_real), dt)
target_freq_resp = h
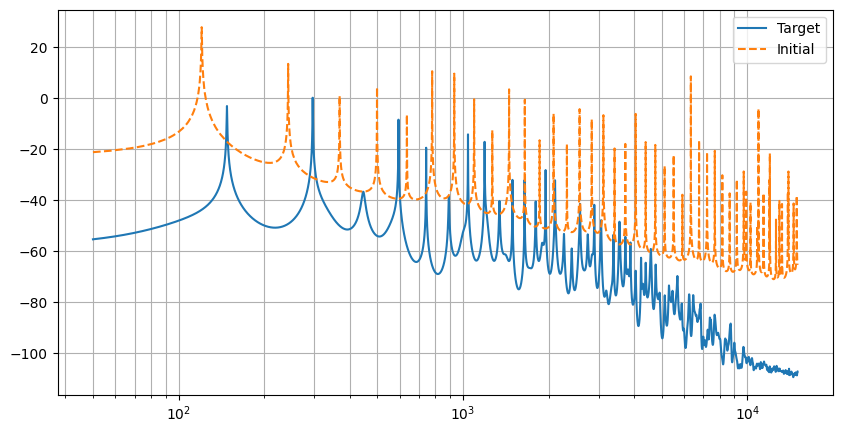
fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.semilogx(
worN,
to_db(target_freq_resp),
label="Target",
)
ax.semilogx(
worN,
to_db(initial_freq_response),
label="Initial",
ls="--",
)
ax.grid(which="both")
_ = ax.legend()
x = jnp.zeros(shape=(sample_rate), dtype=jnp.float32)
x = x.at[0].set(1.0)
mean_sol_pred = iir_filter_parallel(b, a, x).mean(axis=1)
display_audio_with_title(y, sample_rate, "Target")
display_audio_with_title(mean_sol_pred, sample_rate, "Initial")
Target
Initial
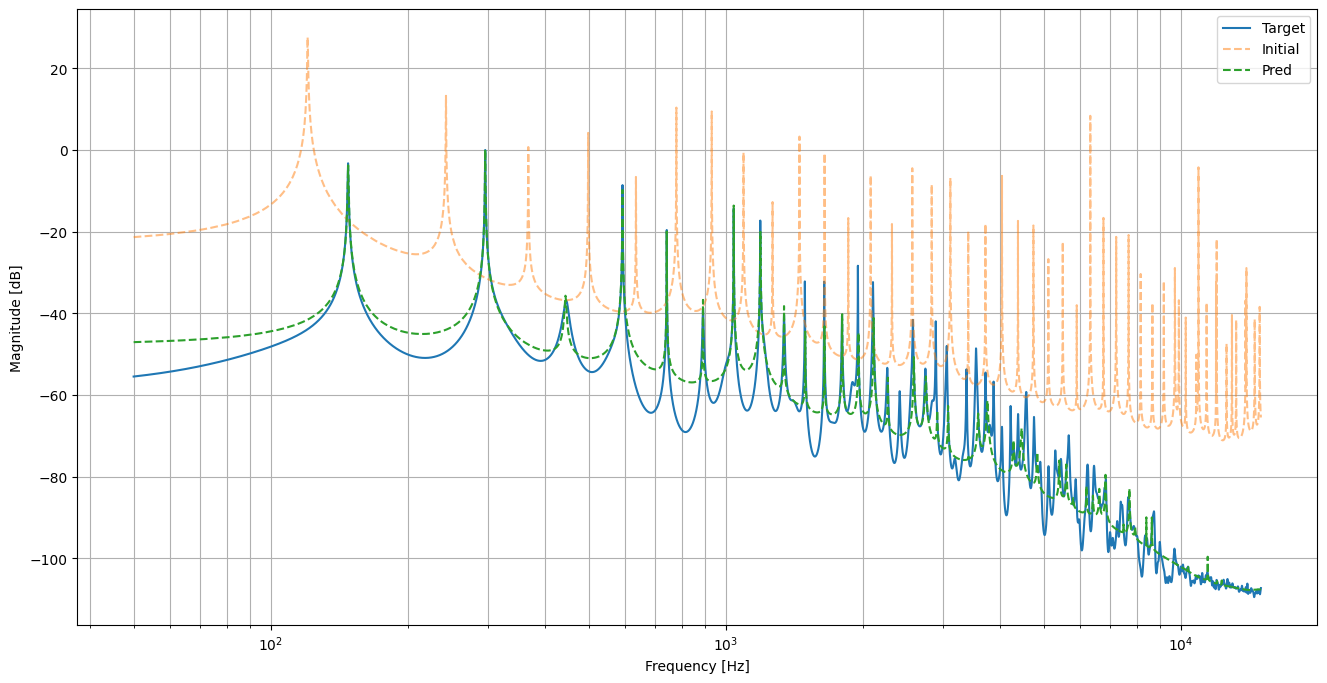
Optimise the parameters using gradient descent.
Code
iterations = 20_000
learning_rate = 3e-2
scheduler = optax.cosine_onecycle_schedule(
transition_steps=iterations,
peak_value=learning_rate,
)
optimiser = optax.chain(
optax.clip_by_global_norm(2.0),
optax.adam(learning_rate=scheduler),
)
state = optimiser.init(pars)
def loss_fn(pars):
pred_freq_resp, b, a = simulate_string(pars)
log_diff = safe_log(pred_freq_resp) - safe_log(target_freq_resp)
log_l1_loss = jnp.mean(
jnp.abs(
log_diff,
),
)
sc_loss = spectral_convergence_loss(
pred_freq_resp,
target_freq_resp,
)
ot_loss = jnp.mean(
spectral_wasserstein(
pred_freq_resp,
target_freq_resp,
is_mag=True,
)
)
return log_l1_loss * 0.1 + sc_loss + ot_loss
@jax.jit
def train_step(pars, state):
loss, grads = jax.value_and_grad(loss_fn)(pars)
updates, state = optimiser.update(grads, state, pars)
pars = optax.apply_updates(pars, updates)
return pars, state, loss
bar = tqdm(range(iterations))
for i in bar:
pars, state, loss = train_step(pars, state)
bar.set_description(
f"Loss: {loss:.3f}, length: {get_length(pars):.3f}, Ts0: {get_Ts0(pars):.3f}, bending stiffness: {get_bending_stiffness(pars):.3f}"
)
Loss: 0.176, length: 0.676, Ts0: 40033.289, bending stiffness: 0.384: 100%|██████████| 20000/20000 [00:34<00:00, 585.55it/s]
Target
Optimised